Chapter 2: Whole Numbers
Exercise 2.3
Q1. Which of the following will not represent zero:
(a) 1 + 0
(b) 0 x 0
(c)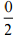 
(d)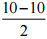 
Answer.
(a) 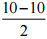is equal to 1
Q2. If the product of two whole numbers is zero, can we say that one or both of them will be zero? Justify through examples.
Answer. Yes, if we multiply any number with zero the resultant product will be zero.
Example: 2 x 0 = 0, 5 x 0 = 0, 8 x 0 = 0
If both numbers are zero, then the result also be zero.
0 x 0 = 0
Q3. If the product of two whole number is 1, can we say that one or both of them will be 1? Justify through examples.
Answer. If only one number be 1 then the product cannot be 1.
Examples: 4 x 1 = 4, 6 x 1 = 6, 8 x 1 = 8
If both number are 1, then the product is 1
1 x 1 = 1
Q4. Find using distributive property:
(a) 728 x 101
(b) 5437 x 1001
(c) 824 x 25
(d) 4275 x 125
(e) 504 x 35
Answer.
(a) 728 x 101
= 728 x (100 + 1)
= 728 x 100 + 728 x 1
= 72800 + 728
= 73528
(b) 5437 x 1001
= 5437 x (1000 + 1)
= 5437 x 1000 + 5437 x 1
= 5437000 + 5437
= 5442437
(c) 824 x 25
= 824 x (20 + 5)
= 824 x 20 + 824 x 5
= 16480 + 4120
= 20600
(d) 4275 x 125
= 4275 x (100 + 20 + 5)
= 4275 x 100 + 4275 x 20 + 4275 x5
= 427500 + 85500 + 21375 = 534375
(e) 504 x 35
= (500 + 4) x 35
= 500 x 35 + 4 x 35
= 17500 + 140
= 17640
Q5. Study the pattern:
1 x 8 + 1 = 9;
12 x 8 + 2 = 98;
123 x 8 + 3 = 987,
1234 x 8 + 4 = 9876;
12345 x 8 + 5 = 98765
Write the next two steps. Can you say how the pattern works?
Answer.
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
Pattern works like this:
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9875643