Scalars Quantities:
Scalars are the physical quantities that have magnitude only.Temperature, speed, mass, and volume are examples of scalars.
Vectors Quantities:
Vectors are the physical quantities that have magnitude and direction.Position, displacement, velocity, acceleration and force are examples of vector quantities.
Representation of a vector:
A vector can be represented by a straight line with an arrow head(→). The length of the vector represents its magnitude and the arrow head indicates its direction.
Note: The physical quantity like electric current possesses both the magnitude and direction, still they are not vectors, and similarly any form of energy is a scalar.
Types of Vector:
1) Zero vector or Null vector: A vector having zero magnitude is called a Null vector or Zero vector.Zero vector has no specific direction.The position vector of origin is a zero vector.
2) Equal vectors: Vectors are said to be equal if both vectors have same magnitude and direction.
3) Parallel vectors (Like vectors): Vectors are said to be parallel if they have the same directions.
Note:
Two equal vectors are always parallel but, two parallel vectors may or may not be equal vectors.
4) Anti parallel vectors (Unlike vectors): Vectors are said to be anti parallel if they acts in opposite direction.
5) Negative vector or Opposite vector : The negative vector of any vector is a vector having equal magnitude but acts in opposite direction.
6) Concurrent vectors (Co-initial vectors ): vectors having the same initial point are called concurrent vectors or co-initial vectors.
7) Co-planar vectors: The vectors in the same plane are called co-planar vectors.
8) Orthogonal vectors: Two vectors are said to be orthogonal to one another if the angle between them is 90°.
9) Co-terminus vectors: vectors having the same terminal point are called co-terminus vectors.
10 ) Position Vector: A vector which gives the position of a point with reference to the origin of the coordinate system is called position vector.
11) Unit vector: A vector having unit magnitude is called unit vector.For example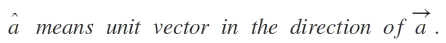 
Mathematically
Mathematically
Note:
-
-
-
When a positive number is multiplied by a unit vector,it becomes a vector of magnitude equal to the magnitude of the number in the direction of the given unit vector.While when a negative number is multiplied by a unit vector,it becomes a vector of magnitude equal to the magnitude of the number in the opposite direction of the given unit vector.
VECTOR ALGEBRA
Contents
hide
1. Addition of vectors: The addition of scalars involves only the addition of their magnitudes. But, when a vector is added with another vector we have to consider their direction also.
A vector can be added with another vector provided both the vectors represents the same physical quantity. For example, the addition of a vector representing displacement of a body with
another vector representing velocity of the body is meaningless.
METHODS OF VECTOR ADDITION:
I .Triangle law of vector addition:
Triangle law of vector addition states that if two vectors can be represented in magnitude and direction by two sides of a triangle taken in the same order, then their resultant
is represented completely by the third side of the triangle taken in opposite order.
II. Parallelogram method of vector addition:
Parallelogram method of vector addition states that if two vectors acting at a point can be represented both in magnitude and direction by the two adjacent sides of a parallelogram drawn from that point, the resultant is represented completely by the diagonal of the parallelogram passing through that point.
To add two vectors placed with common initial point, the parallelogram method of vector is used.
Note:
1) The advantage of the parallelogram method is that one can get both the sum and the difference of two vectors if one knows how to identify the appropriate directions.
2) The resultant of two vectors does not depend on the order in which the vectors are added.
III. Law of polygon of vector addition:
Law of polygon of vector addition states that if a number of vectors are represented both in magnitude and direction by the sides of a polygon taken in the same order, then their sum (resultant) is represented both in magnitude and direction by the closing side of the polygon taken in the opposite order.
2. Subtraction of two vectors:
Example 1
Example 2
Note:Subtraction of one vector with another vector is regarded as the addition of one vector with a negative of another vector.
Resolution Of Vectors:
Resolution of a vector means the process of splitting of a vector into components. If a vector is resolved into two components along the two mutually perpendicular directions, they are called ‘rectangular components’.
Case-I
Two dimensional splitting:
Case-II
Three dimensional splitting:
Dot product of two vectors:
Dot product of two vectors is equal to simple product of first vector and projection of second vector on first vector.
Dot product of unit vectors:
With the help of this table we can find the dot product of unit vectors.
 |
 |
 |
|
 |
1
|
0
|
0
|
 |
0
|
1
|
0
|
 |
0
|
0
|
1
|
Dot product of two given vectors:
Angle between two given vectors:
Properties of dot product:
1. cross product of two vectors obey the commutative law.
2. cross product of two vectors is distributive over vector addition.
Application of dot product:
1. Work done is the dot product of force and displacement.
2. Power is the dot product of force and velocity.
Cross or Vector product of two vectors:
Cross or Vector product of unit vectors:
Vector product of two given vectors:
Properties of vector or cross product:
1. cross product of two vectors does not obey the commutative law.
2. cross product of two vectors is distributive over vector addition.
Application of cross
product:
1. linear velocity is the cross product of angular velocity and displacement.
2. Torque is the cross product of displacement vector and force.